はじめに
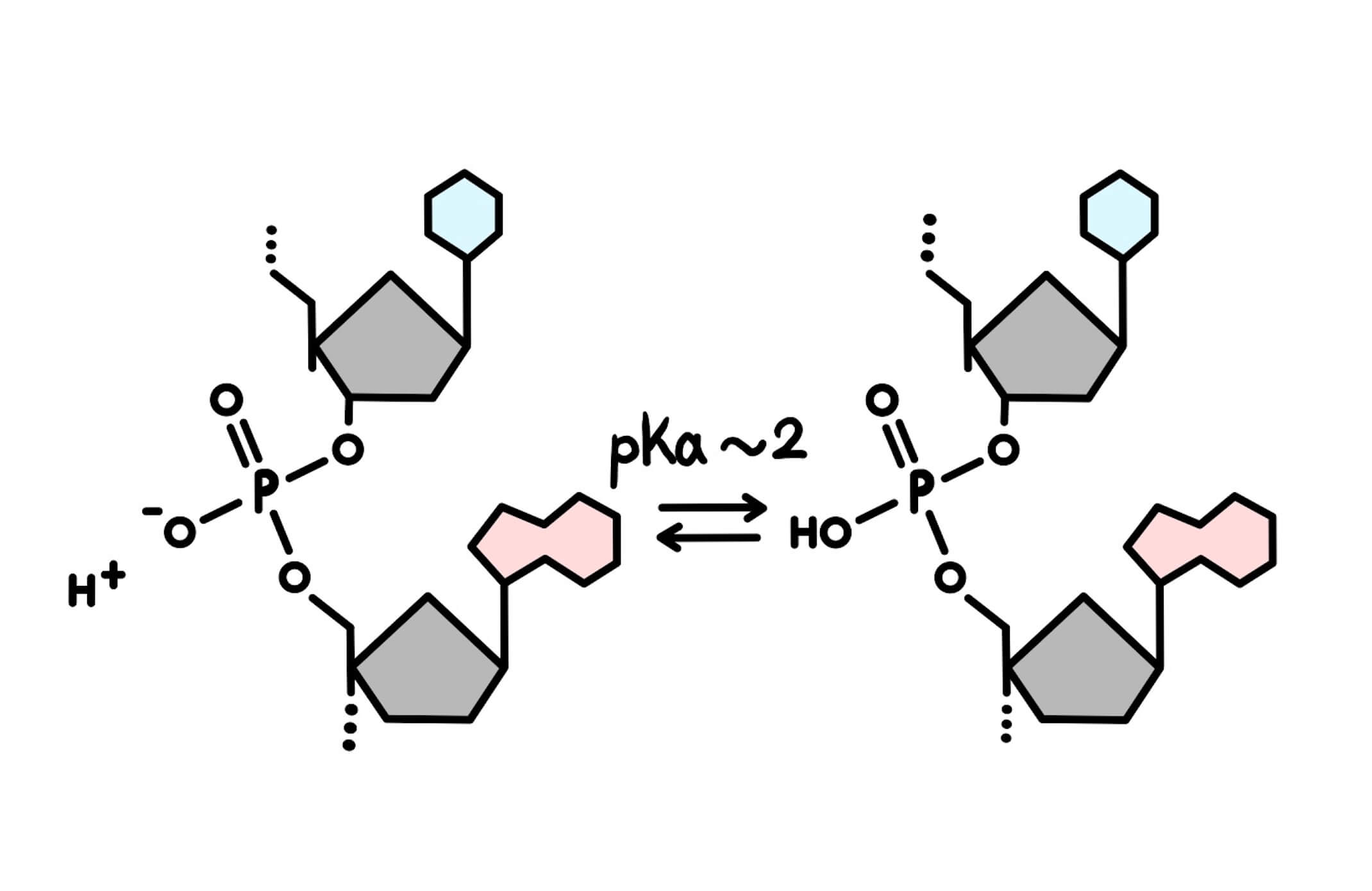
DNAは生理的な条件(=中性条件)では、DNAに含まれるほとんんどのリン酸が電離して負電荷を帯びています。これは、酸に固有の定数である酸解離定数pKaについて学ぶことで、理解することができます!
pKaについて知ることで、教科書に書かれているアミノ酸のカルボキシ基(-COOH)とアミノ基(-NH2)が、電離した形(-COO–と-NH3+)で書かれている理由についてもお分かりいただけると思います。また、緩衝液(バッファー)の原理を学ぶ上でも重要な知識です。
ぜひ最後までご覧ください!
【難易度】★★★☆☆
【重要度】★★★★★
基礎知識の確認
pH
pHは溶液中の水素イオン濃度( = [H+] )を指しており、式①で表します。なぜ水素イオンそのものではなく、水素イオンの常用対数にマイナスをつけたものかというと、水溶液中に含まれる水素イオンは微量(10-0~10-14M)であり、そのままだと扱いづらいからです。
$ \displaystyle\ pH = -log_{10}[H^+] $ … ①
pHは0~14までの値をとります。これはどんな水溶液でも1気圧、25℃において式②の関係が成り立つからです。式②のように、水素イオン濃度[H+]と水酸化イオン濃度[OH–]を掛け合わせたものを水のイオン積と言い、Kwで表します。
$ \displaystyle\ Kw = [H^+][OH^-] = 10^{-14}(mol/L)^2 $ … ②
酸解離定数pKa
酸が式③のように水溶液中で電離しているとき、酸解離定数Kaは式④で表されます。Kaは物質ごとに一定の値をとる定数であり、酸の強さを表す指標となります。
$ \displaystyle\ [HA] \rightleftharpoons[H^+] + [A^-] $ … ③
$ \displaystyle\ Ka={[H^+][A^-]\over[HA]} $ … ④
Kaも値が小さいのでpHと同様に、常用対数にマイナスをつけて式⑤のように表します。強酸ほど水素イオンを放出しやすいので、pKaは小さくなります。
$ \displaystyle\ pKa = -log_{10} Ka $ … ⑤
pHとpKaの関係式
ここで式④を式変形して、pHとpKaの関係式を導出します。
$ \displaystyle\ Ka={[H^+][A^-]\over[HA]} $ … ④
$ \displaystyle\ log_{10}Ka = log_{10}{[H^+][A^-]\over[HA]} $
$ \displaystyle\ log_{10}Ka = log_{10}{[H^+]} + log_{10}{[A^-]\over[HA]} $
$ \displaystyle\ -log_{10}{[H^+]} = -log_{10}Ka + log_{10}{[A^-]\over[HA]} $
$ \displaystyle\ pH = pKa + log_{10}{[A^-]\over[HA]} $ … ⑥
式⑥はヘンダーソン・ハッセルバル式と呼ばれ、水溶液中のpHを予想できる重要な関係式です。
次に式⑥をさらに変形して、[HA]と[A–]の存在比についての関係式を導出します。
$ \displaystyle\ pH = pKa + log_{10}{[A^-]\over[HA]} $ … ⑥
$ \displaystyle\ log_{10}{[A^-]\over[HA]} = pH – pKa $
$ \displaystyle\ log_{10}{[A^-]\over[HA]} = log_{10}10^{pH – pKa} $
$ \displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} $ … ⑦
式⑦より、式③で表した反応がどの程度起きているかわかります。HAのpKaを2だとして、溶液中のpHが変化したとき、HAの電離状態がどのように変化するか見ていきましょう。
pH = 7 の水溶液中のとき
$ \displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} $ … ⑦
$ \displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} = 10^{7 – 2} = 10^5 $
$ \displaystyle\ [A^-] : [HA] = 10^5 : 1 $
つまり、pH = 7 の水溶液中では、
[A-]の存在比 = [H+]の存在比 = $\displaystyle\ {10^5\over 10^5 + 1} \cdot\ 100 \fallingdotseq 100\% $
[HA]の存在比 = $\displaystyle\ {1\over 10^5 + 1} \cdot\ 100 \fallingdotseq 0\% $
のようになり、HAはほぼ100%電離してA–とH+の状態であることがわかります。
pH = 2 の水溶液中のとき
$\displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} $ … ⑦
$\displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} = 10^{2 – 2} = 10^0 = 1 $
$\displaystyle\ [A^-] : [HA] = 1 : 1 $
つまり、pH = 2 の水溶液中では、
[A-]の存在比 = [H+]の存在比 = $\displaystyle\ {1 \over 1 + 1} \cdot\ 100 = 50\% $
[HA]の存在比 = $\displaystyle\ {1 \over 1 + 1} \cdot\ 100 = 50\% $
のようになり、ちょうど半分電離していることがわかります。したがって、pH = pKaのとき、50%のHAがA–とH+に電離しています。
pH = 1 の水溶液中のとき
$\displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} $ … ⑦
$\displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} = 10^{1 – 2} = 10^{-1} = {1 \over 10} $
$\displaystyle\ [A^-] : [HA] = 1 : 10 $
つまり、pH = 1 の水溶液中では、
[A-]の存在比 = [H+]の存在比 = $\displaystyle\ {1 \over 1 + 10} \cdot\ 100 = \fallingdotseq 9\% $
[HA]の存在比 = $\displaystyle\ {10 \over 1 + 10} \cdot\ 100 \fallingdotseq 91\% $
のようになり、HAの約10%が電離していることがわかります。
このように酸解離定数pKaが2であるHAの解離状態を、溶液のpHが0から14まで調べてグラフにプロットすると、図1のようになります。図1からもわかるように、生理的な条件(=中性付近のpH)では、ほぼ100%のHAがHA–とH+に解離していることがわかります。そして溶液のpHを下げるとだんだんとHAの存在比が増え、pH = 2で50%、pH = 1で90%、pH = 0で100%になっています。
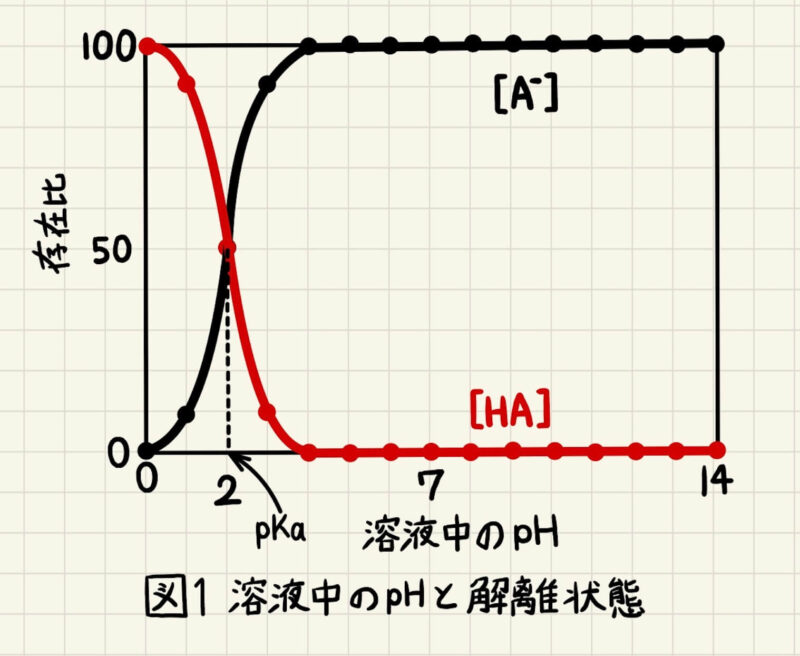

式⑥と図1より、pHを1変化させるためには、HAとA–の比率を10倍変化させる必要があります。したがって、酸または塩基を加えても水溶液中のpHはあまり変化しません。このように溶液中のpHを保つような性質を緩衝作用といいます。pKaとpHが近いほど、緩衝作用が大きくなります。
DNAはなぜ負に帯電しているのか?
酸解離定数pKa = 2の酸の電離状態が、溶液中のpHによってどのように変化するのかを見ていきました。ここで、DNAの構造を見て見ましょう。DNAに含まれているヌクレオチドはリン酸基を介してつながっています(図2)。この結合様式をホスホジエステル結合と呼びます(図2)。
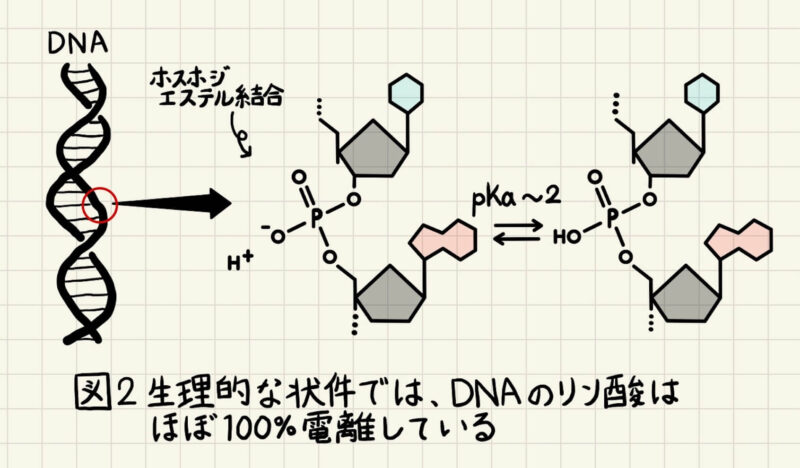
リン酸の電離式は式⑧で表され、この時の酸解離定数はpKa = 2.15となります。
$\displaystyle\ H_{3}PO_{4} \rightleftharpoons {H_{2}PO_{4}}^{-1} + H^+ $ … ⑧
DNA中の糖-リン酸骨格のリン酸は水素ではなく、炭素原子と結合しているので、上記とは少しpKaの値が異なりますが、pKaはだいたい2程度になります。したがって、生理的な条件(=中性条件)では、DNA中のリン酸基はほぼ100%電離しており、常に負に帯電しています(図2)。
まとめ
- pHの定義式:$\displaystyle\ pH = -log_{10}[H^+] $
- 酸解離定数pKaの定義式:$\displaystyle\ pKa = -log_{10}Ka $
- pHとpKaの関係式(ヘンダーソン・ハッセルバル式):$\displaystyle\ pH = pKa + log_{10}{[A^-]\over[HA]} $
- ヘンダーソン・ハッセルバルを変形した式($\displaystyle\ {[A^-]\over[HA]} = 10^{pH – pKa} $)から電離状態を計算できる。
- 糖-リン酸骨格中のリン酸基は生理的な条件(=中性条件)では、ほぼ100%電離している。