はじめに
今回は深層学習の仕組みについて解説します。深層学習は、人工知能(AI)の一分野であり、大規模なデータセットからデータの特徴を学習し、複雑な問題を解決する能力を持っています。深層学習の応用範囲は多岐にわたり、医学分野や生物学の分野にも大きな影響を与えています。例えば、AIを用いた病理画像診断や、タンパク質の立体構造を予測するAlphaFoldなどが挙げられます。今後、AIアルゴリズムや計算機能力の向上により、AI分野はますます発展していくでしょう。
そこで、本記事では深層学習(ディープラーニング)について、基本的な仕組みから数学的な理解までできるように、初学者にもわかりやすく解説していきます!AIを学びたい方や、AIの数学的背景を知りたい方に、ぜひ読んでいただきたい内容となっています。
深層学習の概要
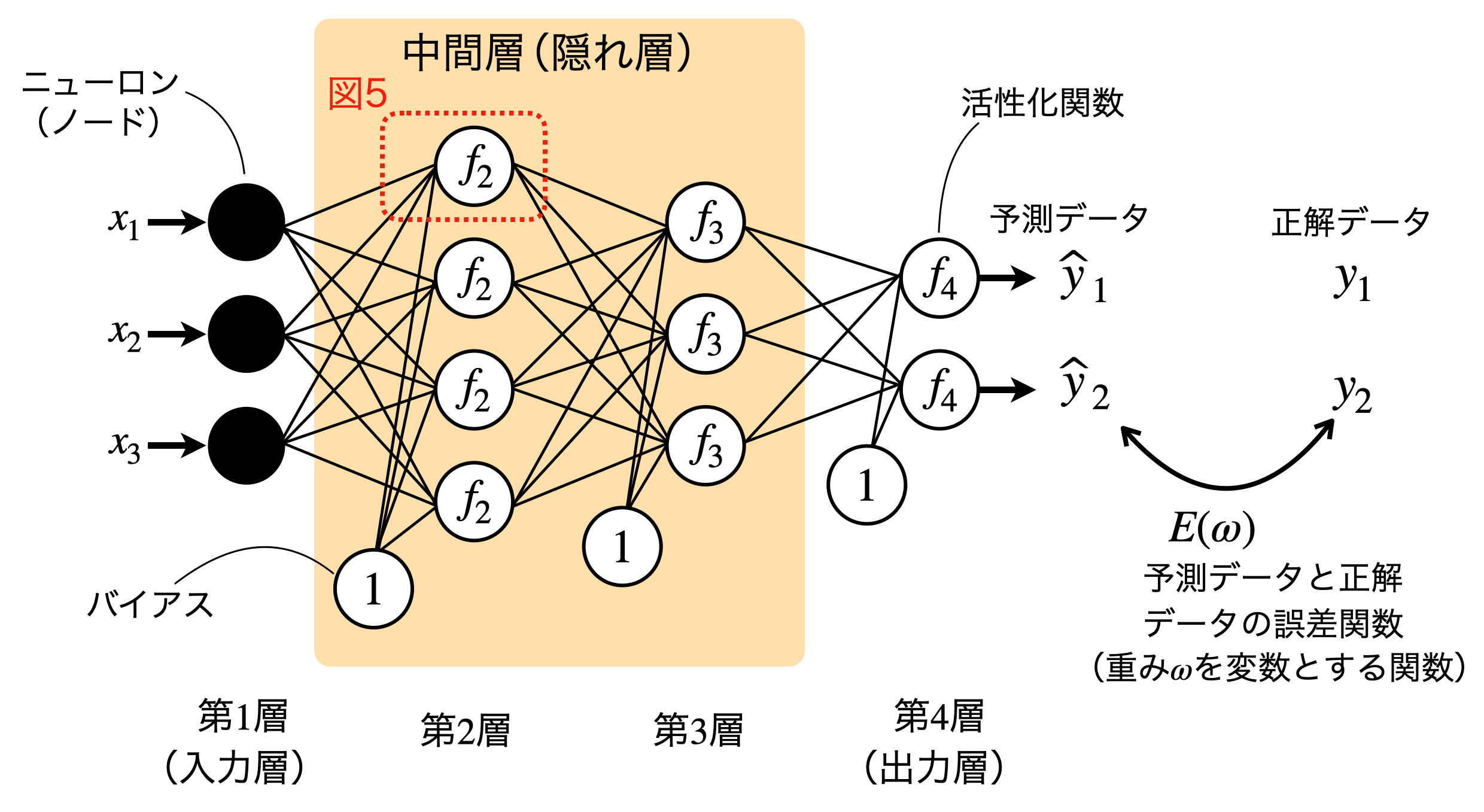
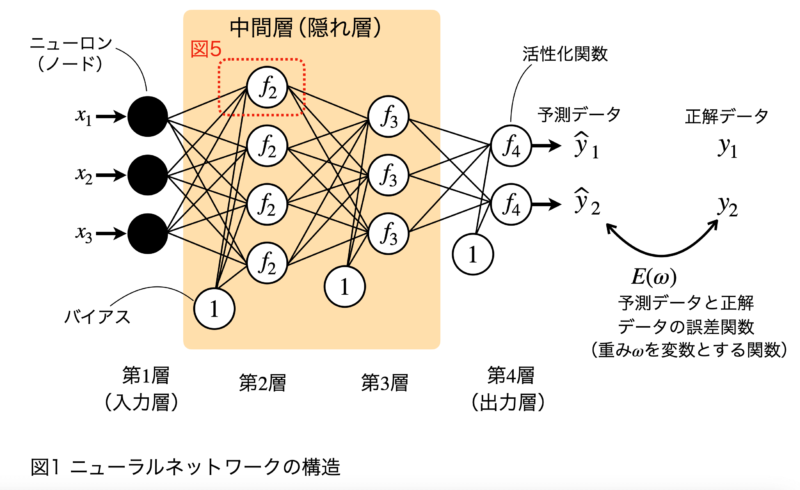
ニューラルネットワークは、人間の神経回路をモデル化した機械学習アルゴリズムです。ニューラルネットワークは、複数のニューロン(ユニットまたはノードと呼ばれる)が層状に配置されており、それぞれのノードは互いに結合しています(図1)。特に図1のように、ある層のユニットすべてが次の層のすべてのユニットと結合している結合形式を全結合層(Dense Layer)と言います。
図1は4層(入力層x1, 中間層x2, 出力層x1)からなるニューラルネットワークの例で、それぞれの層は2~4個のユニットで構成されています。深層学習(ディープラーニング)は、ニューラルネットワークの中間層(隠れ層)を増やしたもの(層が深いと表現します)を言います。「中間層が何層以上であれば深層学習である」という厳密な定義はありません。深層学習は、多層の中間層を持つことにより、より高度な特徴抽出や複雑な関係性を学習することができます。
以降の章では、深層学習を構成するニューラルネットワークの構造や仕組みについて詳しく解説していきます。

与えられた入力データとそれに対応する正解データのペアを使用してモデルを学習させる手法を教師あり学習と言いますが、今回は特に教師あり学習を解説します!
ニューラルネットワークの概要
教師あり学習では入力値と正解値のペアをニューラルネットワークに与えます。ニューラルネットワークは与えられた入力に対して予測を行い、その予測値と正解値の間の誤差を最小化するようにパラメータを調整します。
まず最初に、層の数が1つで、1ユニットからなる単純なニューラルネットワークを使って、ニューラルネットワークの基本的な仕組みや動作原理を解説します。
重み$ \displaystyle\ ω$による線形変換
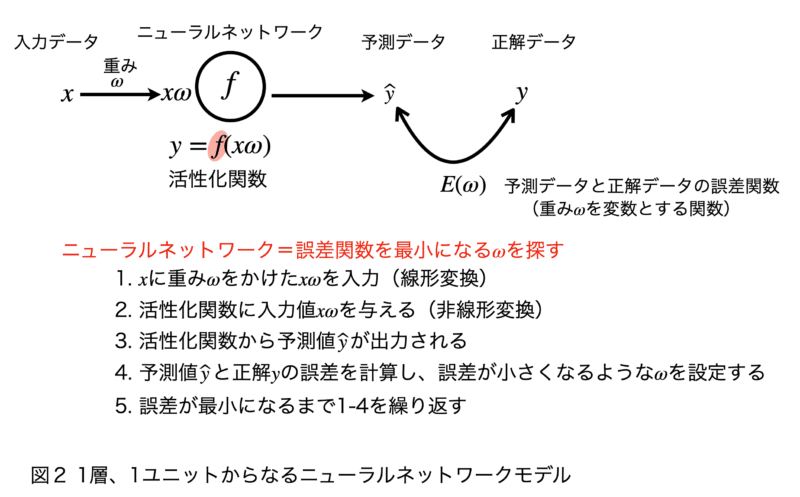
ニューラルネットワークに入力したい値を$ \displaystyle\ x$とすると、入力値は$ \displaystyle\ x$に重み$ \displaystyle\ ω$をかけた$ \displaystyle\ ωx$となります。これは単純な掛け算で、いわゆる線形結合というものです。重み$ \displaystyle\ ω$はノード間の結合の強度を表しています。つまり、入力信号に対する重要度や影響度を示しています(図2)。
今回は入力データが1次元なので重みも1つしかありませんが、通常は複数の入力があり、それぞれの入力に対して重みが存在します。重みを調整することで、入力データから有用な特徴を抽出しているのです。ニューラルネットワークの目的は結局、「重みの組み合わせをいろいろ試し、出力値と正解値の誤差(損失とも呼ばれます)が最小になるような重み を決定する」ということになります。重みをいろいろ試し、最適な重みを探すステップを学習と言います。

図2では省略していますが、入力と重みの積$ \displaystyle\ xω$に加えて、本来はバイアスを加えます(図1)。
したがって、入力値は$ \displaystyle\ xω+b(\text{バイアス})$となります。
活性化関数による非線形変換
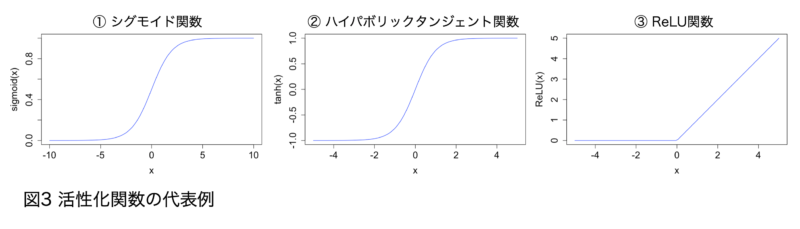
続いて、活性化関数を用いて入力値$ \displaystyle\ xω$を変換します。ニューラルネットワークにおいてよく使用される活性化関数には以下のものがあります。以下の活性化関数の図を見てのとおり、活性化関数は入力値を非線形変換します。活性化関数によって非線形性が導入されることで、ニューラルネットワークはより複雑な表現ができるようになります。
図2は一層ですが、通常のニューラルネットワークは複数の層で構成されています。活性化関数から出力された出力値は、新たな重みがかけられて次のユニットの入力値となります。このように、ニューラルネットワークでは、線形結合と非線形結合を繰り返しでできています。
一般的に同じ層の中では同じ活性化関数が使用されます。
- シグモイド関数:$ \displaystyle\ sigmoid(x)={1\over {1+e^{-x}}}$
シグモイド関数は入力を、0~1の範囲に変換します(図3①)。 - ハイパボリックタンジェント関数:$ \displaystyle\ sigmoid(x)=tanh(x)={e^x+e^{-x}\over {e^x+e^{-x}}}$
ハイパボリックタンジェント関数は入力を、-1~1の範囲に変換します(図3②)。 - ReLU関数:$ \displaystyle\ ReLU(x)=max(0,x)$
ReLU関数(レルと発音します)は、入力が0以下の場合は0を出力し、入力が0より大きければ入力値をそのまま出力します(図3③)。 - ソフトマックス関数:$ \displaystyle\ softmax(x_i)={e^{x_i}\over \sum_{i=1}^ne^{x_i}}$
ソフトマックス関数は通常、出力層で確率的な出力が求めらる時に使用されます。$ \displaystyle\ x_i$は出力層のユニット$ \displaystyle\ i$からの出力で、nはクラス数を表します。全ての出力値の総和で割ることで、各クラスの確率を計算していることになります。ソフトマックス関数は、0~1の出力値で、合計が1になります。これにより、ニューラルネットワークの出力をクラスごとの確率として考えることができます。
例えば、スパムメールを分類したい場合、出力層をソフトマックス関数に設定し、「スパム」または「非スパム」の2つのクラスの確率をソフトマックス関数で計算します。
誤差の最小化
活性化関数によって、予測値$ \displaystyle\ \widehat{y}$が生成されます。この予測値$ \displaystyle\ \widehat{y}$と正解値$ \displaystyle\ y$の誤差を計算する関数を設定します。ニューラルネットワークにおいてよく使用される誤差関数(損失関数)には以下のものがあります。
ニューラルネットワークの学習ステップでは、重みの値をいろいろ試し、誤差関数を最小化する重みを探します。誤差関数が最小になる重みを見つけたとき、ニューラルネットワークの学習が終了し、完成したモデルが得られます。
重みの探索方法ですが、勾配降下法と誤差逆伝播法が用いられます。これらの手法については、次回の記事で解説していきます。
- 平均二乗誤差(Mean Squared Error; MSE):$ \displaystyle\
\begin{split}MSE=\frac{1}n\sum_{i=1}^n(y_i-\widehat{y}_i)^2\
\end{split}$
平均二乗誤差は、予測値と正解値の差の平方の平均を計算します。ここで、nはデータの総数、 は$ \displaystyle\ i$番目の正解値、 $ \displaystyle\ \widehat{y}_i$は$ \displaystyle\ i$番目の予測値です。MSEは予測誤差の大きさを示し、この値が小さいほどモデルの予測精度が高いことを意味しています。MSEを最小化することで、モデルの予測性能を向上させることができます。
- 交差エントロピー誤差(Cross-Entropy Error; CE):\begin{split}CE=-\sum_{i=1}^ny_ilog(\widehat{y}_i)\
\end{split}
交差エントロピー誤差は、上記の式で計算します。交差エントロピー誤差は、特に分類問題でよく使用されます。交差エントロピー誤差を計算する式には、自然対数が入っており、予測値と正解値の間の差異が大きい場合に、その誤差をより大きく反映します。

統計学やAIの分野では、予測値であることを「 (ハット)」をつけて表します。
ニューラルネットワークの例
4項では、3項で解説したニューラルネットワークを、具体例を用いて復習していきます。
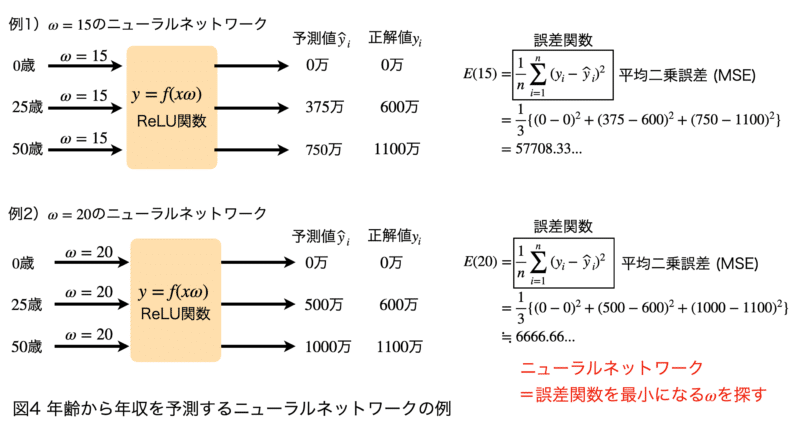
図4は、1層、1ユニットからなる「年齢から年収を予測するニューラルネットワークモデル」です。このモデルでは、活性化関数としてReLU関数、誤差関数として平均二乗誤差を使用しました。
例1)では重みを$ \displaystyle\ ω=15$とし、入力データ(0歳、25歳、50歳)に重みをかけてニューラルネットワークに入れていきます。ReLU関数は、$ \displaystyle\ x\leqq0$のときは0、$ \displaystyle\ x>0$のときは$ \displaystyle\ x$を返す関数ですので、0歳、25歳、50歳の入力データを入れると出力はそれぞれ、$ \displaystyle\ 0=15\times0$、$ \displaystyle\ 375=15\times25$、$ \displaystyle\ 750=15\times50$となります。正解データを0万、600万、1100万とすると、平均二乗誤差は57,708.33…となります。
例2)では重みを$ \displaystyle\ ω=20$に変更しています。例1と同様にして平均二乗誤差を求めると、6,666.66…となります。重みを変化させることで、誤差関数の値が約50,000小さくなっていることがわかります。
このように、ニューラルネットワークの目標は、誤差関数の値が小さくなるような重みを探すということです。
ニューラルネットワークの一般化
通常、ニューラルネットワークは多層、複数ユニットで構成されており、専門書を読んでいるとニューラルネットワークを一般化した式が頻繁に登場します。そこで最後に、ニューラルネットワークを一般化した場合の式について解説していきたいと思います。
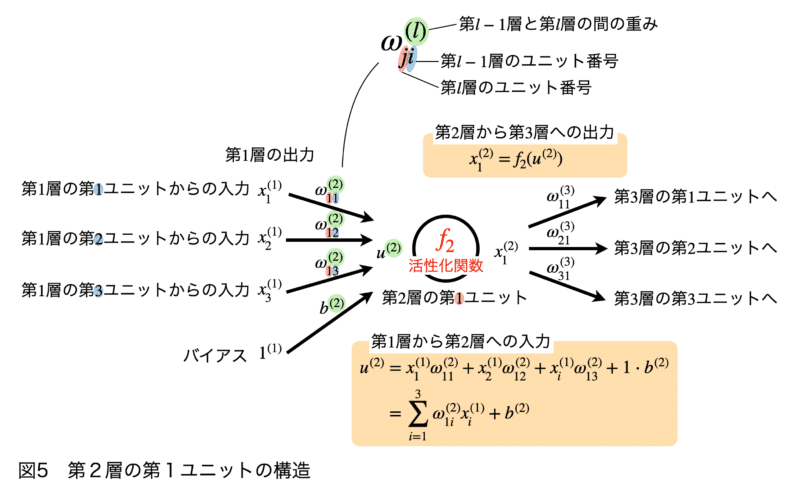
図5は、図1中の第2層の第1ユニットを中心に、周辺のニューラルネットワークの構造を図示しています。
第1層(入力層)
第1層は入力層と呼ばれ、この例では各入力ユニットはそれぞれ$ \displaystyle\ x^{(1)}_1$、$ \displaystyle\ x^{(1)}_2$、$ \displaystyle\ x^{(1)}_3$を受け取ります。右上のカッコ内の数字は、第1層への入力値であることを示しています。右下の数字は、その値を出力しているユニットを示しています。入力値の次元数はデータの次元数と一致します。すなわち、入力データが3次元であれば、入力ユニット数も3となります。入力データが100次元であれば、入力ユニット数も100となります。一般的に、入力層は重み、活性化関数を適用せず、入力をそのまま第2層へ出力します。
第2層(隠れ層)
入力層と出力層の間の層は中間層または隠れ層と呼ばれます。
第2層の一番上の第1ユニット(図1中の赤い点線で囲まれた部位)を例に、ニューラルネットワークにおけるユニットの役割を解説します(図5)。
第2層のユニットは、入力層から出力された入力$ \displaystyle\ x^{(1)}_1$、$ \displaystyle\ x^{(1)}_2$、$ \displaystyle\ x^{(1)}_3$およびバイアス$ \displaystyle\ b^{(1)}$を受け取ります。この時、ニューラルネットワークの各接続には重み$ \displaystyle\ ω^{(1)}_{ji}$がかけられます。重み$ \displaystyle\ ω^{(1)}_{ji}$のカッコ内の数字は、第1層と第2層の間の重みであることを示し、右下の添え字は結合している前後のユニット番号を示しています。例えば、第1層、第2ユニットからの出力値にかけられる重みは$ \displaystyle\ ω^{(2)}_{12}$と表します。
入力層から第2層の第1ユニットへ入力される値を$ \displaystyle\ u^{(2)}$とすると、$ \displaystyle\ u^{(2)}$は前の層からの重みつき入力値を全て足し合わせたものであり、下記の式で表します。
$ \displaystyle\ \begin{equation}\begin{split} u^{(2)}&=x^{(1)}_1ω^{(2)}_{11}+x^{(1)}_2ω^{(2)}_{12}+x^{(1)}_3ω^{(2)}_{13}+1\cdot b^{(2)}\\&=\sum_{i=1}^3x^{(1)}_iω^{(2)}_{1i}+b^{(2)} \ \end{split}\end{equation} $
また、入力$ \displaystyle\ \bf X=\begin{pmatrix}x_1^{(1)} \\x_2^{(1)} \\x_3^{(1)}\\1\end{pmatrix}$、重み$ \displaystyle\ \bf W=\begin{pmatrix}ω^{(2)}_{11} \\ω^{(2)}_{12} \\ω^{(2)}_{13} \\b^{(2)}\end{pmatrix}$と列ベクトルで定義すると、入力値$ \displaystyle\ u^{(2)}$は、下記のように表すことができます。
$ \displaystyle\ u^{(2)}=\begin{pmatrix}ω^{(2)}_{11} \ \ ω^{(2)}_{12} \ \ ω^{(2)}_{13} \ \ 1 \end{pmatrix}$$ \displaystyle\ \begin{pmatrix}x^{(1)}_1 \\x^{(1)}_2 \\x^{(1)}_3 \\b^{(1)} \end{pmatrix}=\bf W^{T}{\bf X}$
Tはベクトルの転置を意味しています。AIの勉強をしていると、上記のようにベクトルの転置を使用して表記する記法が頻繁に使用されます。
続いて、入力値$ \displaystyle\ u^{(2)}$を活性化関数と呼ばれる関数に入れ、入力値を出力値に変換します。ユニットの中の$ \displaystyle\ f_2$は、第2層の活性化関関数であることを意味しています。出力された数値は、次の層のユニットへの入力値として使われていきます。ニューラルネットワークは、このような繰り返し構造となっています。すなわち、各層から出力される値を$ \displaystyle\ y$とすると、ニューラルネットワークは下記の合成関数の式で表すことができます。
$ \displaystyle\ \begin{equation}\begin{split}y&=f^{(4)}(f^{(3)}(f^{(2)}(u^{(2)})))\\&=f^{(4)}(f^{(3)}(f^{(2)}(\sum_{i=1}^3x^{(1)}_iω^{(2)}_{1i}+b^{(2)})))\end{split}\end{equation}$

ニューラルネットワークの正体は、複雑な合成関数なのです!
第$\displaystyle\ l$層
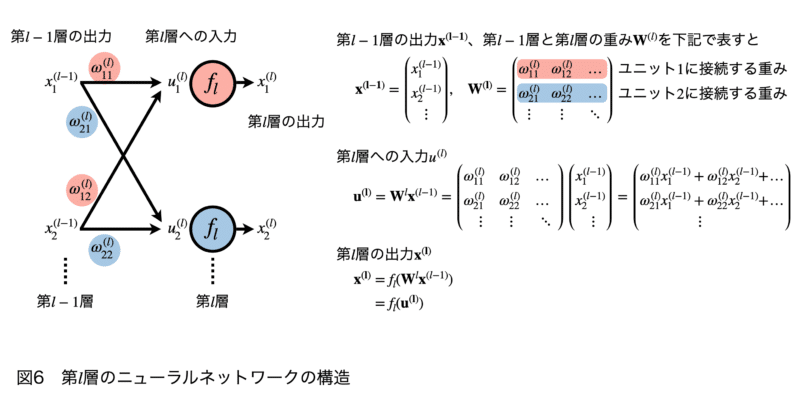
最後に、さらに一般化して第$\displaystyle\ l$層について考えます(図6)。これまでの表記よりも複雑になりますが、数学的な内容はシンプルです。どこの値がどこに使用され、どこへつながっているかという流れを意識して見ていただきたいと思います。
パワメータは、前項と同様に下記のように定義します。また、以降で使用している太字は、ベクトルまたは行列を意味しています。
- $\displaystyle\ x_{1}^{(l-1)}$:第$\displaystyle\ l-1$層、第1ユニットからの出力
- $\displaystyle\ ω^{(l)}_{ji}$:第$\displaystyle\ l-1$層と第$\displaystyle\ l$層の間の重みを、jは第$\displaystyle\ l-1$層のユニット番号、iは$\displaystyle\ l$層のユニット番号
- $\displaystyle\ u_1^{(l)}$:$\displaystyle\ l$層、第1ユニットへの入力値
- $\displaystyle\ x_{1}^{(l)}$:$\displaystyle\ l$層、第1ユニットからの出力
また、$\displaystyle\ l-1$の全てのユニットから出力される出力値を$ \displaystyle\ \bf x^{(l-1)}=\begin{pmatrix}x_1^{(l-1)} \\x_2^{(l-1)} \\ \vdots \end{pmatrix}$、$\displaystyle\ l-1$層~$\displaystyle\ l$層間の全ての重みを $ \displaystyle\ {\bf W^{(l)}}=\begin{pmatrix}ω_{11}^{(l)} & ω_{12}^{(l)} & \dots\\ ω_{21}^{(l)} & ω_{22}^{(l)} & \dots \\ \vdots & \vdots & \ddots \ \end{pmatrix}$とベクトルと行列で定義してみます。
すると、第$\displaystyle\ l$層への入力$\displaystyle\ \bf u^{(l)}$は、下記のように表記することができます。
$ \displaystyle\ \begin{equation}\begin{split} {\bf u^{(l)}}={\bf W}^l{\bf x}^{(l-1)}=\begin{pmatrix}ω_{11}^{(l)} & ω_{12}^{(l)} & \dots\\ ω_{21}^{(l)} & ω_{22}^{(l)} & \dots \\ \vdots & \vdots & \ddots \ \end{pmatrix}\end{split}\end{equation}\begin{pmatrix}x_1^{(l-1)} \\x_2^{(l-1)} \\ \vdots \end{pmatrix}=\begin{pmatrix}ω_{11}^{(l)} x_{1}^{(l-1)} + ω_{12}^{(l)}x_{2}^{(l-1)} + & \dots \\ω_{21}^{(l)}x_{1}^{(l-1)} + ω_{22}^{(l)}x_{2}^{(l-1)}+ & \dots \\ \vdots\:\:\ \end{pmatrix}$
第$\displaystyle\ l$層への入力第$\displaystyle\ \bf u^{(l)}$層は、活性化関数$\displaystyle\ f_l$によって変換されるので、第$\displaystyle\ l$層からの出力$\displaystyle\ {\bf x^{(l)}}$は、下記のように表記することができます。このように、複数の層、複数のユニットからなるニューラルネットワークは、行列を使って表記するとシンプルな数式で表すことができます。
$\displaystyle\ \begin{equation}\begin{split}{\bf x^{(l)}}&=f_l{({\bf W}^l{\bf x}^{(l-1)}})=f_l{({\bf u^{(l)}})}\end{split}\end{equation}$

今回解説したモデルのように、情報が情報が一方向にのみ伝播するニューラルネットワークを順伝播型ニューラルネットワーク(Feedforward Neural Network)といいます。
まとめ
- ニューラルネットワークは、人間の神経回路をモデル化した機械学習アルゴリズム
- 深層学習は、ニューラルネットワークの中間層(隠れ層)を増やしたもの
- ニューラルネットワークは、訓練データを用いてモデルのパラメータ(重み)を調整し、予測値と正解値の誤差を最小化することを目指す
- 入力データは重みをかけた後、足し合わされて次の層のユニットに入力される(線形変換)
- ユニットでは入力値を活性化関数により非線形変換を行う
- ニューラルネットワークは、入力値に対して非線形変換と非線形変換を繰り返し適用することで、より高度な特徴抽出や複雑な関係性を学習することがでる
- 予測値と正解値の誤差を最小化するために、勾配降下法と誤差逆伝播法が使用される